Remote Sensing Lab 7

Goal and Background - The goal of this lab is to learn the skills of Photogrammetry, Stereoscopy, and Orthorectification. These are all practiced using the program Erdas Imagine 2013.

Methods and Results - The first part of the lab was about scale, measurements, and relief displacement. We took a photo of Eau Claire, WI and found the scale of the image by measuring a feature with a ruler and then extrapolating the scale against the actual size of the feature. We also found how to determine the scale with just the altitude of the aerial photograph and the focal lens length. The equation is: Scale equals focal lens length divided by the altitude of the aircraft minus the ground elevation. Next we measured the perimeter and the area of a local lagoon by digitizing the lagoon into a polygon. The last section of the first part was dealing with relief displacement. The object that is displaced is a smokestack in Eau Claire. The smokestack appears to be leaning because it is not close enough to the principal point which is the point underneath the aircraft when the picture was taken. The equation for that is as follows: Relief Displacement equals height of object in real life multiplied by the radial distance in the image divided by the height of aerial camera above datum. The radial distance is the distance between the principal point and the object. Now, once the relief displacement is calculated you can adjust the object to lean towards or away from the principal point.

The second part of the lab was learning to make a stereoscopic image in Erdas Imagine. I took a image of Eau Claire and a digital elevation model (DEM) file of Eau Claire and using the Anaglyph Generation tool I created a new file. The new file when looked at with polaroid glasses, conveys a 3D image of the area.

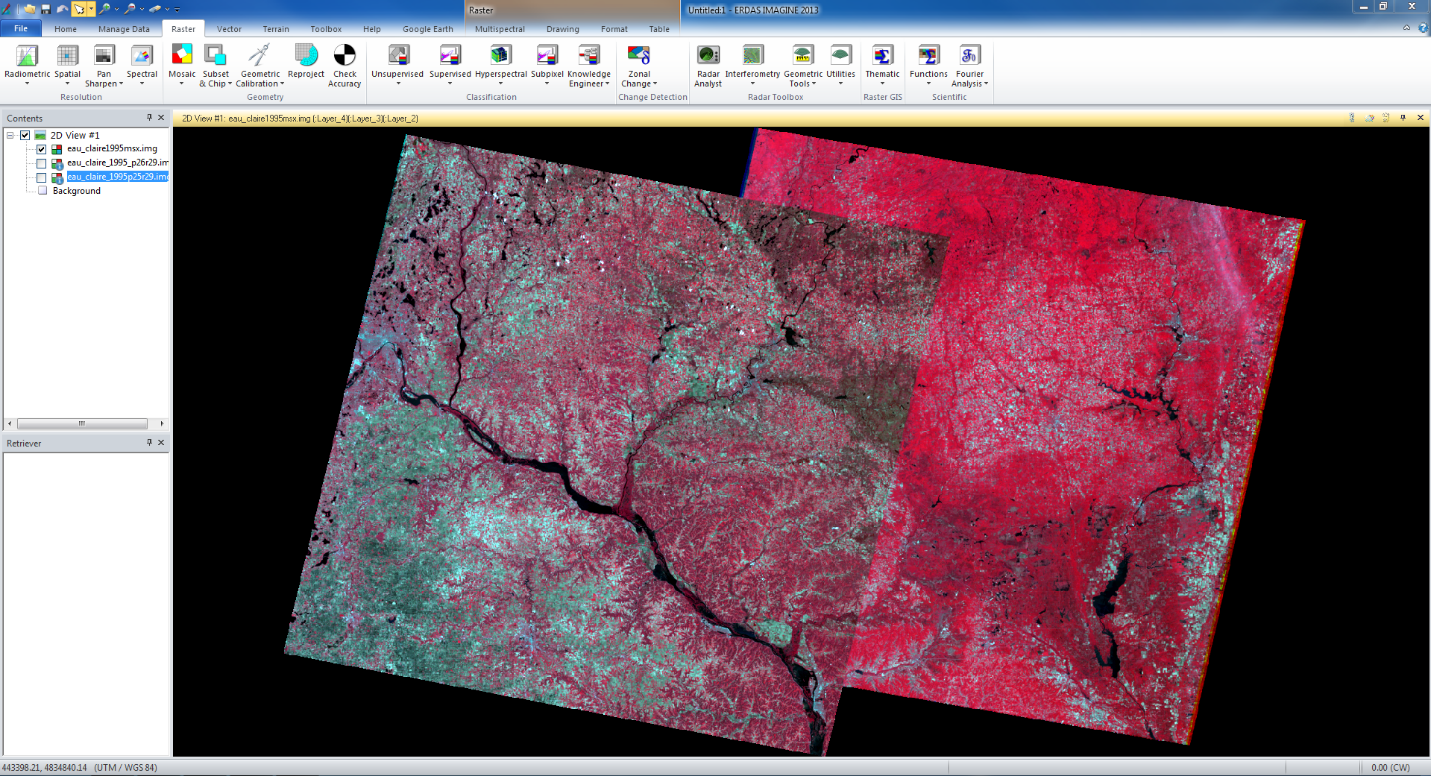
In the third and final part of the lab, we learned Orthorectification using Erdas Imagine Lecia Photogrammetric Suite (LPS). We had two images of an area that overlap each other, however they currently do not match up. To match them up we first took the first image and created twelve GCPs to connect the image to a datum and a projected coordinate system. Next I used a elevation DEM to add the elevation of each point in the data. I then did the same process with the second image matching it up with the first and therefore both had the correct coordinate data. In figure 1 it shows the first twelve points that I connect to both images.


fig 1

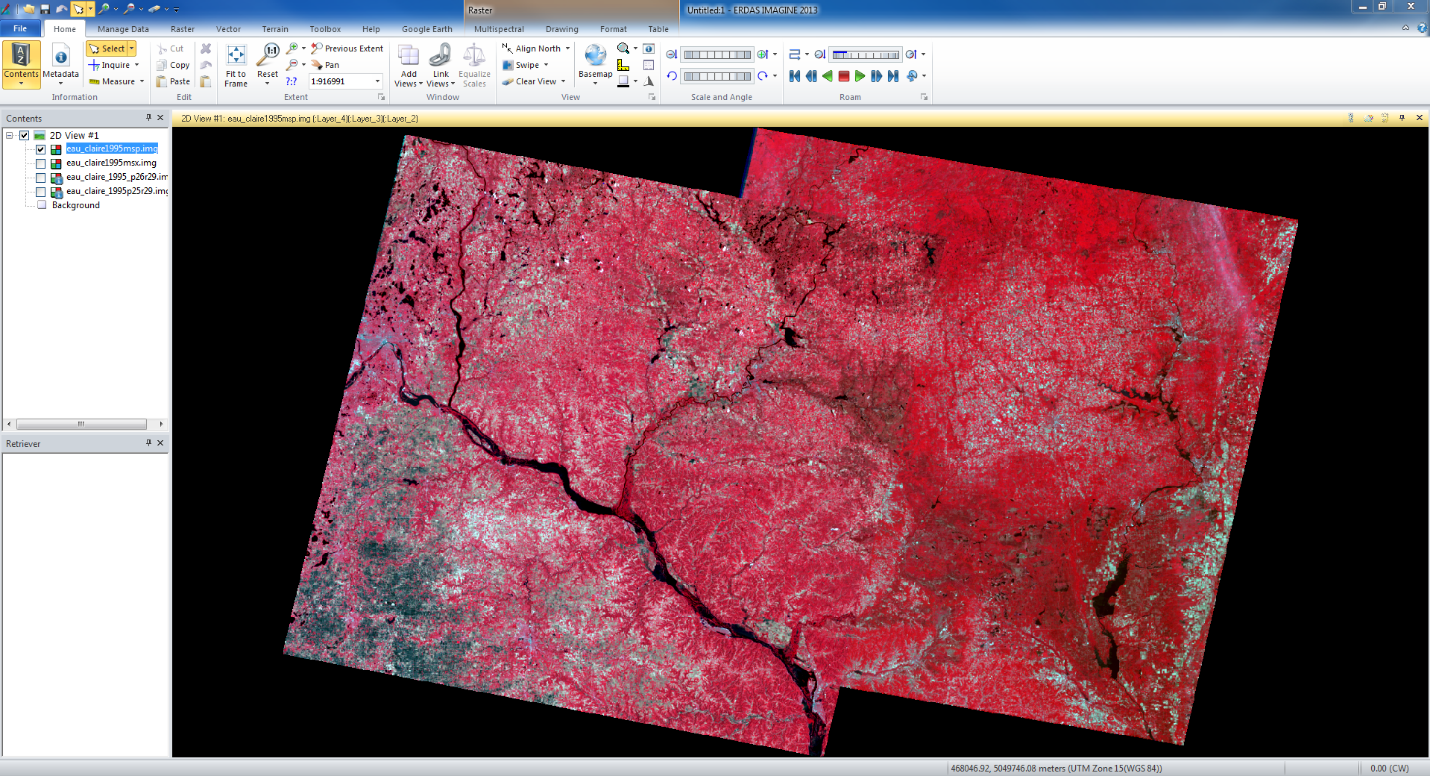
Next we used the automatic tie point generator to connect the images and then the Triangulation tool. The output LPS screen is show below in figure 2.

fig 2

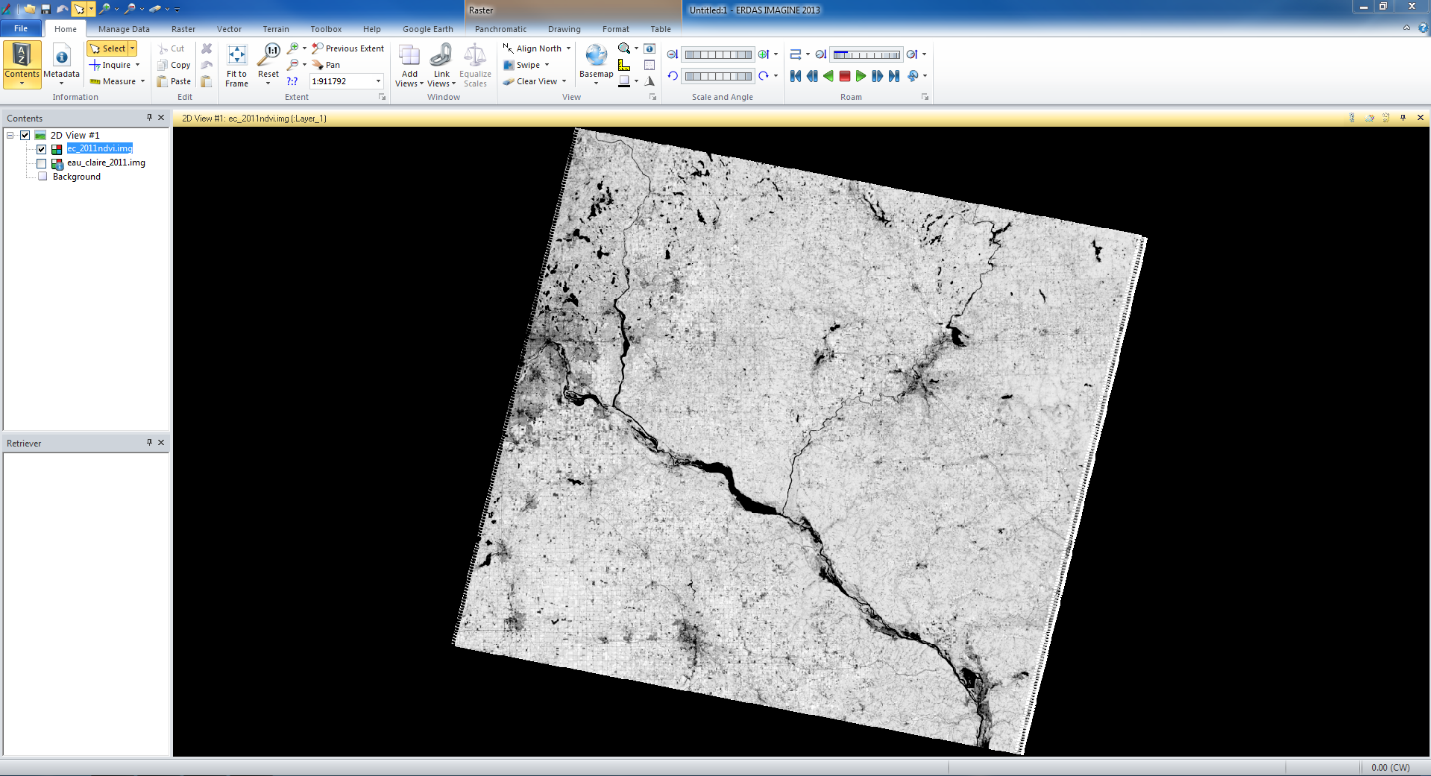
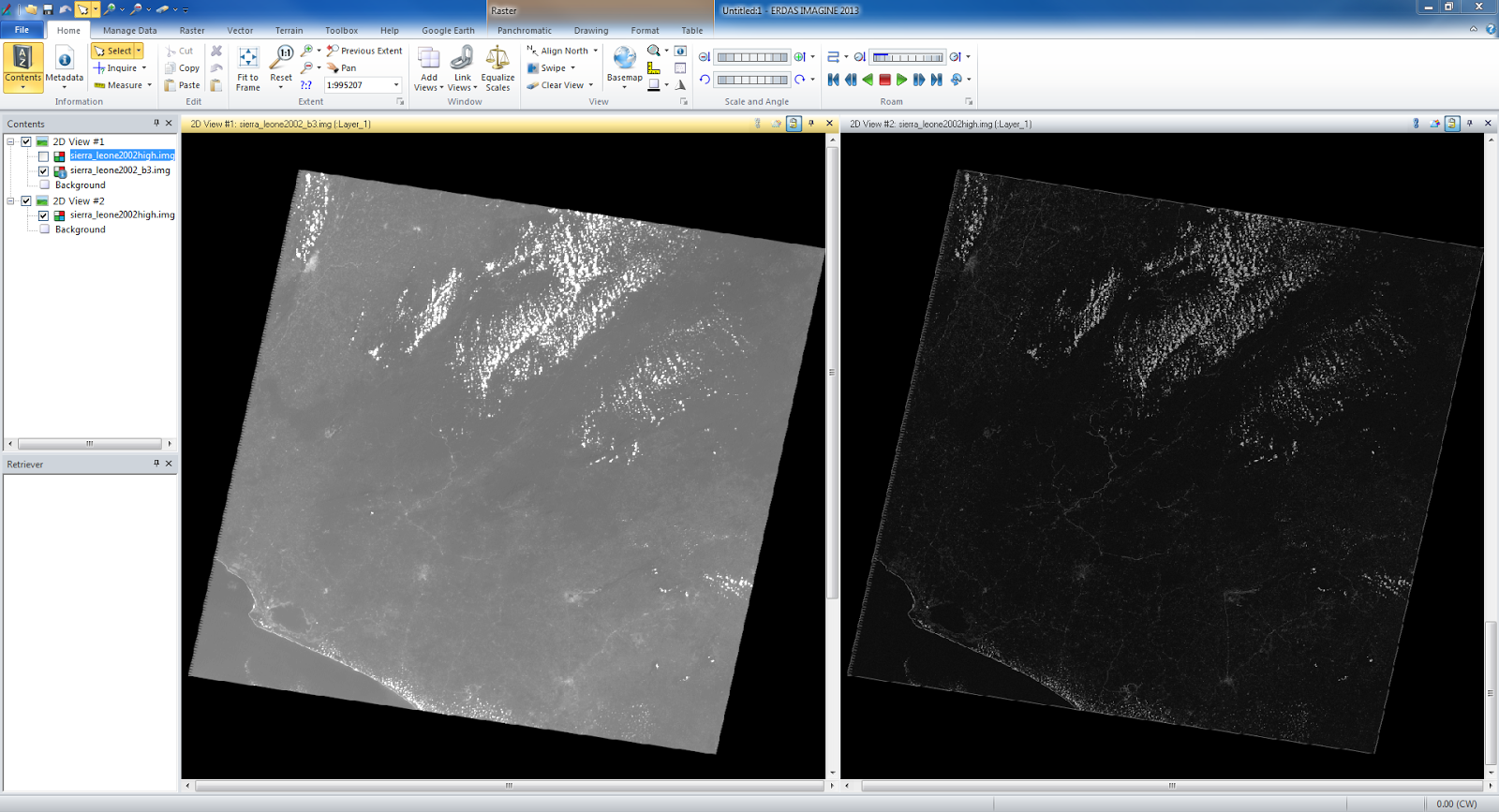
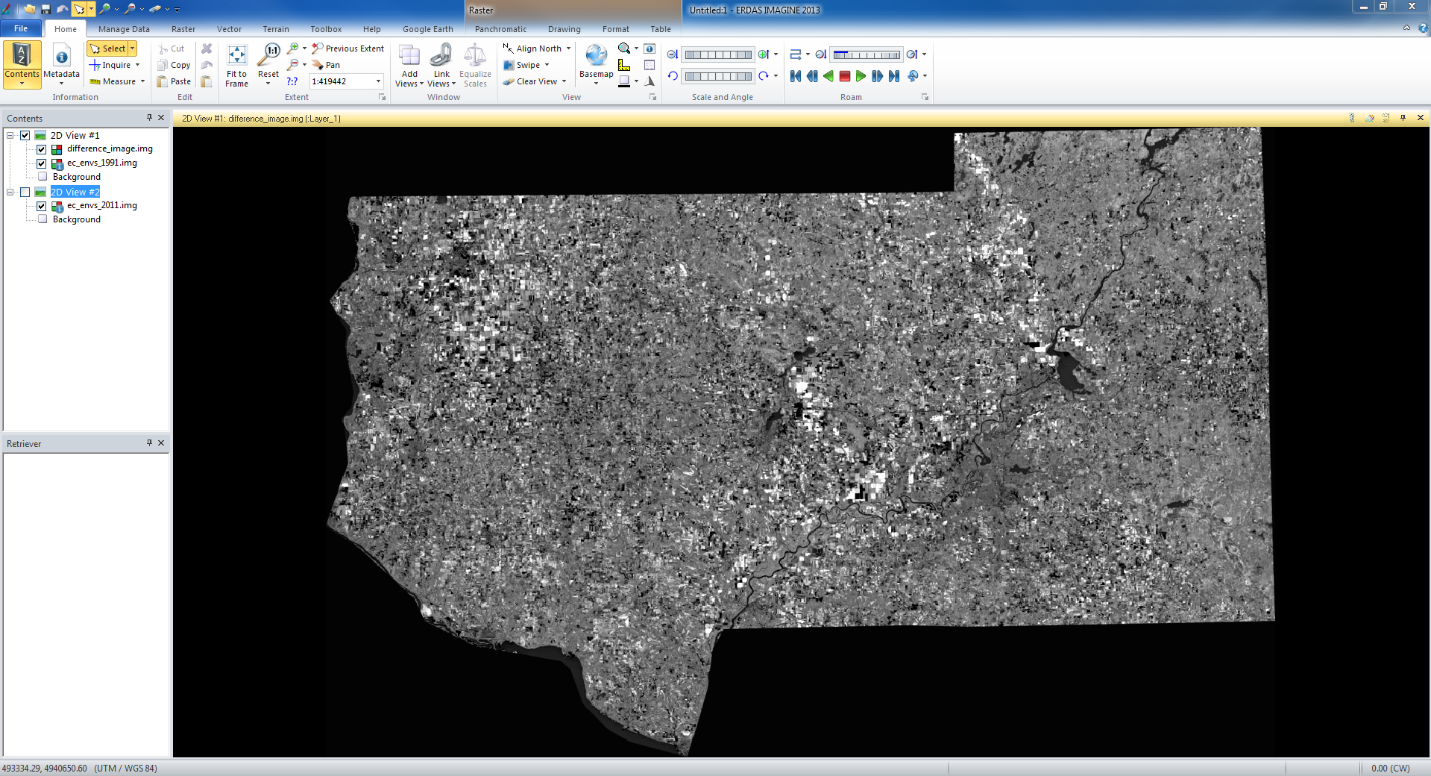
Lastly I brought the images in the viewer in Erdas to see if the images boundaries were fixed and accurate. The image below (fig 3) shows the two images with their new projections.


fig 3

The degree of accuracy at the boundaries of the images is very high. From zoomed out you can see a line between the images, but when zoomed in you can barely even tell the where the two images border at certain areas. The boundary twists and turns on the west border over the mountains and creates a twisting and super accurate boundary.

Sources - All satellite images provided by Cyril Wilson.

Remote Sensing Lab 6

Goal and Background - The goal of this lab is to practice geometric correction. There are two types of geometric correction; Image-to-map rectification and Image-to-image registration. These are both used in the program Erdas Imagine 2013.

Methods and Results - We first took an image of Chicago from 2000 that was distorted and we wanted to correct the image and we first took a topographic image of the Chicago area and brought it into Erdas with the distorted satellite image. Using image-to-map rectification we will be able to correct this image. We opened up the Geometric Correction tool and selected a first order polynomial model with a nearest neighbor resampling method. Since this is a first order polynomial model we only need three ground control points or GCPs, but we should always do more than the minimum, so we'll use four. The image below (fig 1) shows the four GCPs. We then perform the Geometric Correction and our output image is no longer distorted.

fig 1

In the second part of the lab we use a severely distorted image of a region in Sierra Leone in 1991. For this image we will be using the image-to-image registration method. Since this is more distorted than the pervious image we will be using a third order polynomial model with a bilinear interpolation resampling method. Since this is a third order polynomial it is more complex and will require at least ten GCPs, therefore we will use twelve to be on the safe side. The image below (fig 2) shows the twelve GCPs. We then perform the Geometric Correction and our output image is no longer distorted.

fig 2

Sources - All satellite images provided by Cyril Wilson.

Remote Sensing Lab 5

Goal and Background - This lab focused on analytic processes such as image enhancement, binary change detetion, image mosaic, band ratio, and spatial modeling. All of these within the context of Erdas Imagine 2013.

Methods and Results - The first skill we learned was image mosaics. I took two satellite images that over lap spatially both taken in May 1995. We first used the Mosaic Express tool (fig. 1) and then using the MosaicPro tool (fig. 2). The one made using the MosaicPro comes out better due to the use of Color Corrections which blended the two images more smoothly along the shared boundaries.

fig. 1

fig. 2

The second section deals with Band Ratios. We used the normalized difference vegetation index (NDVI) on an image of the Eau Claire area (fig. 3). It shows vegetation as the very white portions of the output image. The dark areas indicate rivers, roads, urban areas, and less healthy vegetation.

fig. 3

The next part introduced us to spatial image enhancement. The low frequency image from Sierra Leone on the left (fig. 4) shows how it is hard to see details when their is little contrast. The image on the right is the enhanced image and shows much more contrast. It is a very dark image, but we learn how to fix that in a later part.

fig. 4

We then performed a Laplacian convoultion filter on another image of Sierra Leone (fig. 5) which increases the contrast at discontinuities. It brings out features such as roads, cities and rivers.

fig. 5

In the next section we practiced spectral enhancement. We performed minimum-maximum contrast stretch (fig. 6) on an image of Eau Claire that had a Gaussian histogram. On the second image of Eau Claire which was an NIR image we used a piecewise contrast stretch (fig. 7). We also performed a Histogram Equalization which spread a low frequency histogram across the whole range creating a high contrast image.

fig. 6

fig. 7

The final part dealt with binary change detection and image difference. We took an image of the Eau Claire region from 1991 and another of the same area from 2011 and we wanted to find the parts that changed in those 20 years. We first created a difference image (fig. 8) to show what pixels changed from 1991 to 2011.

fig. 8

 We then used the Model Maker tool to create a model that got rid of the pixels that stayed the same from 1991 to 2011 and created a difference image that only showed the areas that changed in the time period. I then opened ArcMap and overlaying the image of the changed area on top of a map of the region (fig. 9) showing the areas that changed in the region between 1991 and 2011 in red. It showed that the areas that changed were all agricultural lands.

fig. 9

Sources - All satellite images provided by Cyril Wilson.